|
|
|
The derivation of the equations of motion of damped and driven pendula extends the derivation of the undamped and undriven case. Damping and driving are caused by two additional forces acting on the pendulum: The damping force and the driving force.
An undamped pendulum can be realized only virtually as here in the Pendulum Lab. In reality dissipation of energy
leading to damping is unavoidable. Usually dissipation is included in the equation of motion by adding a viscous
damping term which is a damping constant times the velocity. Thus, the equation of motion of the damped pendulum
reads
| (1) |
d2 |
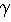 is the damping
constant. Such a force occurs, for example, when a sphere is dragged through a viscous medium (a fluid or a gas).
For a laminar flow (i.e., a flow without eddies) the dragging force is given by Stoke's law
is the damping
constant. Such a force occurs, for example, when a sphere is dragged through a viscous medium (a fluid or a gas).
For a laminar flow (i.e., a flow without eddies) the dragging force is given by Stoke's law 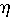 Rv,
Rv,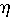 is the viscosity of the medium, R
is the radius of the sphere, and v is its velocity relative to the medium.
is the viscosity of the medium, R
is the radius of the sphere, and v is its velocity relative to the medium.
In general, different damping mechanisms of different strengths are possible. Imagine, e.g., a heavy spherical
mass which hangs at a thin wire rope from the ceiling. Here, the main sources of damping are aerodynamical friction
due to the motion of the mass through the air and friction caused by bending the rope at the suspension point.
Aerodynamical friction follows Stoke's law only for very small velocities. For large velocities, when the flow becomes
turbulent, the friction force increases roughly quadratically. The friction of the rope is caused by plastic deformation
and solid friction if it is made by many fibres.
In both cases, the friction force may dependent on the velocity and other parameters in
a complicated way. In general, a viscous damping force is usually only a phenomenological
force. Even if it is empirically correct, it is often difficult to calculate the damping constant. Here in the Pendulum
Lab, the damping force is always the viscous damping term 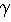 d
d![]() /dt
/dt
There are several ways to drive a pendulum. The most simplest one is to add a periodic force. This leads to
| (periodic force) |
d2 |
Additional comments:
| QUESTIONS worth to think about: |
|