The Harmonic Oscillator
The harmonic oscillator is a canonical system discussed in every
freshman course of physics. Thus, you might skip this lecture if you are
familiar with it.
1. Basic equations of motion and solutions
The linearized equation of motion of an undamped and undriven pendulum is called a
harmonic oscillator:
Nearly all oscillators and oscillations in physics are modeled by this equation of motion, at least in a first
approximation, because it can be solved analytically. It is a linear second-order
differential equation with constant coefficients.
Such a differential equation can be solved easily by the ansatz
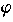 = exp(
= exp(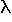 t), where
t), where 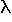 is some constant which has to be calculated. Each d/dt
puts a factor
is some constant which has to be calculated. Each d/dt
puts a factor 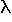 before the exponential
function. Thus, a linear ordinary differential equation like (1)
turns into a polynomial because the
common exponential function (a nonzero factor) can be dropped. Thus,
before the exponential
function. Thus, a linear ordinary differential equation like (1)
turns into a polynomial because the
common exponential function (a nonzero factor) can be dropped. Thus, 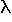 2 +
2 +  02 = 0. The roots
of this so-called characteristic polynomial are
02 = 0. The roots
of this so-called characteristic polynomial are 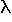 = ±i
= ±i 0. Hence, we get two solutions. Because the equation of motion is
linear, one gets new solutions by multiplying a known solution by an arbitrary factor or by adding a solution
to another one. This so-called superposition principle of linear differential equations is very powerful.
It says that any solution can be built up by only a few different types of "building blocks" called
fundamental solutions. The solutions exp(-i
0. Hence, we get two solutions. Because the equation of motion is
linear, one gets new solutions by multiplying a known solution by an arbitrary factor or by adding a solution
to another one. This so-called superposition principle of linear differential equations is very powerful.
It says that any solution can be built up by only a few different types of "building blocks" called
fundamental solutions. The solutions exp(-i 0t) and exp(+i
0t) and exp(+i 0t) are a set of two independent
fundamental solutions of the harmonic oscillator. Thus, the general solution of (1) reads
0t) are a set of two independent
fundamental solutions of the harmonic oscillator. Thus, the general solution of (1) reads
where C is a complex number and C* denotes its conjugated complex. Because of the superposition
principle, the set of fundamental solutions can be arbitrary, except that a fundamental solution has to be independent
from the other ones. That is, each fundamental solution can not be written as a weighted
sum of the other fundamental solutions. Instead of the complex
valued exponential functions, one often chooses sin( 0t)=(exp(i
0t)=(exp(i 0t)-exp(-i
0t)-exp(-i 0t))/2i and cos(
0t))/2i and cos( 0t)=(exp(i
0t)=(exp(i 0t)+exp(-i
0t)+exp(-i 0t))/2 as another
set of fundamental solutions. Therefore,
0t))/2 as another
set of fundamental solutions. Therefore,
is a general solution, too. The constants A and B can be expressed in term of C and vice versa.
 Using the porperties of trigonometric functions,
the general solution can also be expressed in a physically more relevant way: Using the porperties of trigonometric functions,
the general solution can also be expressed in a physically more relevant way:
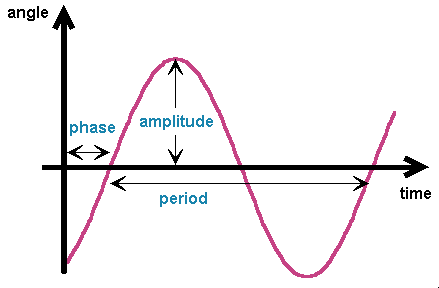
where 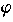 max
and max
and 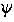 are the amplitude and the phase of oscillation, respectively. Again they can be expressed in terms
of the integration constants of (2) or (3). Note, that these constants are determined
by the initial conditions
are the amplitude and the phase of oscillation, respectively. Again they can be expressed in terms
of the integration constants of (2) or (3). Note, that these constants are determined
by the initial conditions 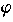 (0) and d (0) and d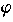 /dt|0. The period of oscillation is T0=2 /dt|0. The period of oscillation is T0=2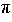 / / 0. These three quantities are independent from each
other. This isn't a triviality as nonlinear
oscillations show. In fact, the independence of the frequency from the
amplitude is a more subtile definition of a harmonic oscillator. 0. These three quantities are independent from each
other. This isn't a triviality as nonlinear
oscillations show. In fact, the independence of the frequency from the
amplitude is a more subtile definition of a harmonic oscillator. |
2. Damping
What happens if the harmonic oscilliator is damped? In this case, the equation of motions has an additional term which
comes from the damping force:
Again, with the ansatz 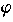 = exp(
= exp(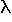 t),
one gets a characteristic polynomial:
t),
one gets a characteristic polynomial:
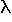 2 +
2 + 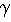
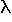 +
+  02
= 0. It has the solutions
02
= 0. It has the solutions
3. Resonance
Oscillations in a damped harmonic oscillator decay to zero. When it is
driven by a periodic force, one oscillation survives.
The equation of motion of a damped and driven harmonic oscillator reads
This is still a linear differential equation, but the sum of two solutions are no longer a solution. The reason
for that is the inhomogenous term on the right-hand side. Nevertheless, the superposition principle holds
in a modified version. A solution of (9) plus an arbitray solution of
(5) (a so-called homogeneous solution)
is also a solution of (9).
One needs only one solution of (9) (the so-called particular
solution) to generate any solution of
(9) with the help of the homogeneous solution. Here, a particular solution can be found by the ansatz
It turns (9) into a sum with terms proportionally to cos(2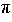 f t) and sin(2
f t) and sin(2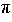 f t). Because the equation should hold for any value of t,
the sum of all cosinus terms and the sum of all sinus terms have to be zero independently. Hence, [
f t). Because the equation should hold for any value of t,
the sum of all cosinus terms and the sum of all sinus terms have to be zero independently. Hence, [ 02-(2
02-(2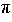 f)2] B + 2
f)2] B + 2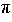 f
f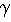 A = a and [
A = a and [ 02-(2
02-(2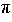 f)2] A - 2
f)2] A - 2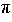 f
f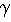 B = 0, respectively. The solution of these
equations reads
B = 0, respectively. The solution of these
equations reads
In the long-time limit any solution of (9) approaches the particular solution (10)
since any solution of (5) decays to zero. The harmonic oscillator, therefore, oscillates not
with its eigenfrequency  0 but with the frequency of the periodic force. The amplitude of oscillations
depend on the driving frequency. It has its maximum when the driving frequency matches the eigenfrequency. This
phenomenon is called resonance. To see this, rewrite equation (10) in the form
0 but with the frequency of the periodic force. The amplitude of oscillations
depend on the driving frequency. It has its maximum when the driving frequency matches the eigenfrequency. This
phenomenon is called resonance. To see this, rewrite equation (10) in the form 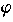 (t) =
(t) = 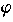 max cos(2
max cos(2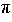 ft-
ft-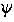 ), with
), with
and
In the underdamped case, the amplitude as a function of the driving frequency has a maximum near the eigenfrequency f0
=  0/2
0/2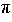 of the oscillator. The deviation
is of quadratic order in
of the oscillator. The deviation
is of quadratic order in 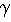 . The maximum
is a/(
. The maximum
is a/( 0
0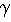 ) in leading order of
) in leading order of 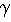 . This is by a factor
. This is by a factor  0/
0/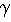 larger than the amplitude for f
larger than the amplitude for f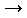 0. That is, the amplitude of oscillation is larger
than the amplitude of driving. This can be easily observed in the lab at the horizontally driven
pendulum. The width of the so-called resonance line is proportional to
0. That is, the amplitude of oscillation is larger
than the amplitude of driving. This can be easily observed in the lab at the horizontally driven
pendulum. The width of the so-called resonance line is proportional to 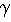 . In the critically damped and overdamped case the resonance line disappears.
. In the critically damped and overdamped case the resonance line disappears.
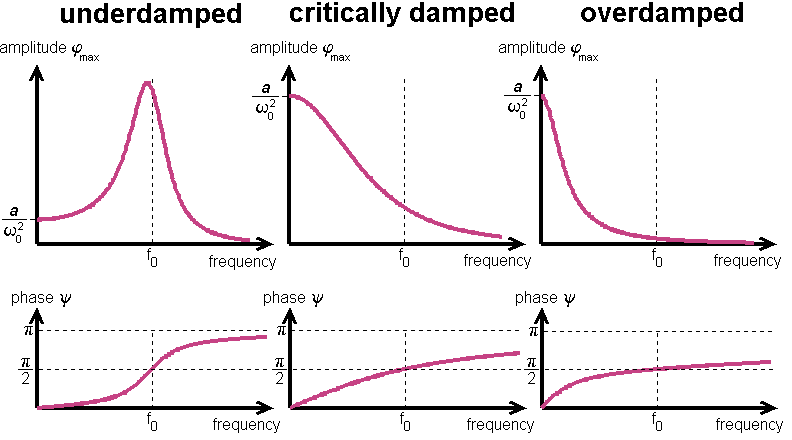
In the limit f 0 the phase of oscillation is identical with the driving phase. In resonance, the phase is just 90° behind the driving
phase. At high frequencies the phase approaches 180°.
Thus, the pendulum moves just opposite to the drive. Again,
this can be easily observed in the lab
at the horizontally driven pendulum.
0 the phase of oscillation is identical with the driving phase. In resonance, the phase is just 90° behind the driving
phase. At high frequencies the phase approaches 180°.
Thus, the pendulum moves just opposite to the drive. Again,
this can be easily observed in the lab
at the horizontally driven pendulum.
| QUESTIONS worth to think about: |
- What happens with an undamped harmonic oscillator driven exactly by its eigenfrequency?
- Another look at the dynamics of the damped and driven harmonic oscillator
is the following one: Instead of discussing the solution as a function of
time, discuss it as a function of the initial conditions. For example,
calculate the angle and the angular velocity at a given time as a function
of the angle and the angluar velocity for the previous period of driving. That is,
given are the initial conditions
 (0)
and d (0)
and d /dt|0.
Calculate /dt|0.
Calculate 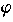 (1/f)
and d (1/f)
and d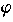 /dt|1/f
as a function of the initial conditions. This calculation leads to
a Poincaré map or stroboscopic map. /dt|1/f
as a function of the initial conditions. This calculation leads to
a Poincaré map or stroboscopic map.
|
© 1998 Franz-Josef Elmer,  elmer@ubaclu.unibas.ch
last modified Sunday, July 19, 1998.
elmer@ubaclu.unibas.ch
last modified Sunday, July 19, 1998.
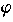 = exp(
= exp(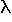 t),
t),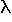 is some constant which has to be calculated. Each
is some constant which has to be calculated. Each 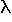 before the exponential
function. Thus, a linear ordinary differential equation like (1)
turns into a polynomial because the
common exponential function (a nonzero factor) can be dropped. Thus,
before the exponential
function. Thus, a linear ordinary differential equation like (1)
turns into a polynomial because the
common exponential function (a nonzero factor) can be dropped. Thus, 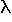 2 +
2 +  02 = 0.
02 = 0.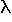 = ±i
= ±i 0.
0. 0t)
0t) 0t)
0t) 0t)=(exp(i
0t)=(exp(i 0t)-exp(-i
0t)-exp(-i 0t))/2i
0t))/2i 0t)=(exp(i
0t)=(exp(i 0t)+exp(-i
0t)+exp(-i 0t))/2
0t))/2 Using the porperties of trigonometric functions,
the general solution can also be expressed in a physically more relevant way:
Using the porperties of trigonometric functions,
the general solution can also be expressed in a physically more relevant way: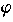 max
max
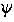
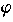 (0)
(0)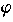 /dt|0
/dt|0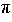 /
/ 0.
0.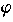 = exp(
= exp(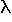 t),
t),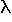 2 +
2 + 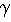
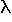 +
+  02
= 0.
02
= 0.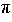 f t)
f t)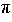 f t).
f t). 02-(2
02-(2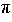 f)2] B + 2
f)2] B + 2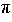 f
f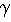 A = a
A = a 02-(2
02-(2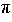 f)2] A - 2
f)2] A - 2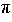 f
f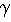 B = 0,
B = 0, 0
0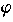 (t) =
(t) = 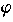 max cos(2
max cos(2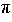 ft-
ft-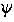 )
) 0/2
0/2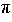
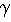 . The maximum
is
. The maximum
is  0
0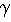 )
)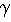 . This is by a factor
. This is by a factor  0/
0/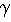
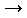 0.
0.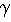 . In the critically damped and overdamped case the resonance line disappears.
. In the critically damped and overdamped case the resonance line disappears.

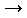 0
0