Research Areas

Quantum entanglement is at the heart of many fundamental problems of quantum information and its various applications. Despite intense research in the previous two or three decades, there remain several gaps in our understanding of entanglement and entanglement measures. Focussing on the case of multipartite systems, we intend to address some of the gaps in entanglement theory such as finding new classes of absolutely maximally entangled (AME) states. The problem of AME states is related to the construction of perfect tensors that are relevant to tensor networks. These have direct bearing on the construction of Quantum Error Correcting Codes. However, these results only scratch the surface of the connections between tensor networks and quantum codes. We aim to gain a better understanding of these connections, with a view to exploiting the tools of tensor networks to solve problems in quantum coding theory and vice versa. Our studies in this area will also have implications for many-body systems including quantum devices and quantum matter.

Much like entanglement, the existence of complementary aspects is a unique feature of quantum theory. Mutually Unbiased Bases (MUBs) are at the heart of investigations into complementarity and incompatibility in quantum systems. Such bases play an important role in quantum information theory and are central to quantum cryptographic tasks such as quantum key distribution. An important open question for finite dimensional quantum systems is the existence and number of MUBs in composite dimensions, the smallest being d=6. We intend to shed some light on this long standing open problem by studying incomplete, but unextendible sets of MUBs in finite dimensional Hilbert spaces. The existence and constructions of MUBs is related to several fundamental mathematical questions such as the existence of Mutually Orthogonal Latin squares, Hadamard matrices, maximal abelian subalgebras.

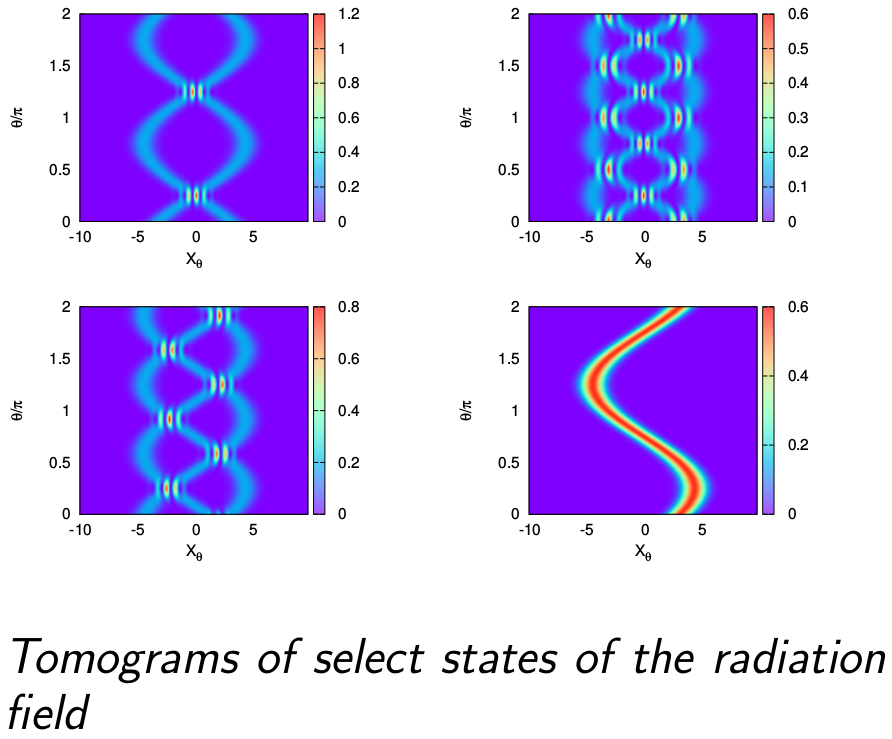
Attempts are currently being made in leading laboratories across the world to create specific entangled states experimentally. Entanglement as a resource is being investigated in atomic, molecular and continuous variable systems in considerable detail, and preliminary investigations are currently being made on entanglement in nuclear systems as well, although this poses special challenges because of strongly interacting substructures such as quarks and gluons. Understanding nuclear structure is complicated by the interplay of different energy scales corresponding to low, medium and heavy nuclei, their collective motion, matter existing inside neutron stars etc. The many-body techniques used theoretically are scale-dependent. It is therefore important to develop a novel approach for obtaining connections between these different many-body techniques, and hence shed light on how to carry out ab-initio calculations. The approach to understanding the structure of many-particle aggregates and collection of spins based on quantum entanglement, is of immense current interest. We note that, quantum state reconstruction from experimentally available tomograms (optical or spin/qubit tomograms) poses several challenges even in few body systems. Reconstruction techniques are inherently error-prone due to the statistical procedures used. A more efficient and useful program would be to extract as much information as possible about the density matrix solely from appropriate tomograms. This approach would involve extraction of bipartite and multipartite indicators directly from tomograms. The usefulness of such a procedure would be most evident in the context of systems with large Hilbert spaces as happens in many-body systems and bound states of several nuclei.

This program is expected to help set metrics for ab-initio calculations for coupled systems of finite nuclei and particle aggregates. While these are certainly novel aspects in the interface of quantum information and nuclear physics, the most audacious element of the proposal deals with extending these investigations to neutron star structure, such as, aspects of pairing and the BEC-BCS crossover. We will use emergent techniques such as tensor networks and holographic duality to study correlated electron systems. The information gleaned will also be used to understand the relation of sign problem encountered in quantum Monte-Carlo based simulation of quantum systems to the entanglement entropy of competing ground states.

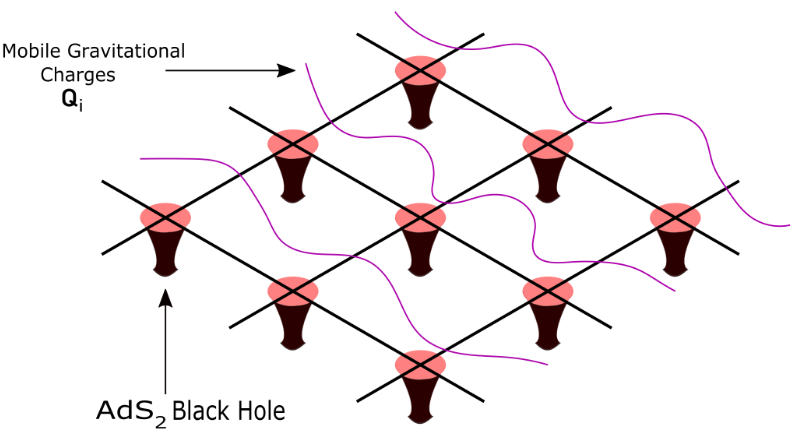
The holographic duality of string theory has been one of the most significant developments in understanding both quantum gravity and quantum field theories which cannot be described in terms of weakly interacting quasiparticles. It gives a precise realization of the holographic principle which posits that quantum spacetime and its dynamics can be encoded in terms of a field theory living on its boundary. Quantum information theory has led to fundamental breakthroughs in understanding of this duality, especially related to how subregions of the emergent spacetime can be decoded from the field theory. The proposal that the encoding of spacetime in the field-theoretic degrees of freedom is essentially an error correcting code has resolved many inconsistencies following from properties of operator algebras, however a more precise formulation is still elusive. The understanding of how quantum black hole interiors can be reconstructed from the dual field theory and information paradoxes resolved still pose the most formidable open challenges in quantum gravity. Tractable holographic models with crucial inputs from QIT are expected to revolutionise our understanding of quantum black holes and also the fundamentals of the holographic duality.

Many basic properties of quantum field theories, such as how the effective descriptions evolve with coarse-graining, how low can the energy-momentum densities be generically, etc have been addressed by QIT inputs pertaining to entanglement properties. However, the computation of entanglement measures, and elucidating the quantum thermodynamic properties of states in field theories pose open problems. The most formidable challenge is to understand if one can simulate quantum field theories in real time in controlled approximations with discrete qubits. Decode the principles of constructing such quantum circuits should also lead us todiscover generalisations of the tensor networks and the holographic duality which have indeed helped immensely in understanding some strongly correlated systems.